- Tree 말단 노드까지의 가장 짧은 경로(DFS) 2022.12.11
- 이진트리 순회(너비우선탐색 : 레벨탐색) 2022.12.10
- 부분집합 구하기(DFS) 2022.12.10
- 이진트리 순회(깊이우선 탐색) 2022.12.10
- 12월 목표 2022.12.06
- 2022.12.06 2022.12.06
- 2022.12.04 2022.12.04
- ISTQB foundation level Ch4-4. 경험 기반 테스트 기법 2022.11.23

말단 노드란 어떠한 자식 노드도 없는 노드를 말한다.
보통 최단 거리, 경로를 찾는 문제는 BFS를 사용하는 것이 좋다. 그러나 DFS와 BFS를 배우는 입장에서 이번 게시물은 DFS를 사용해서 가장 짧은 경로를 구해볼 것이다.
먼저 왼쪽의 트리로 DFS와 BFS를 비교해보자면,


DFS의 경우에는,
자식노드가 null일 때까지 거리를 1씩 더해가면서 재귀함수를 호출한다. 말단노드에 이르면 거리를 반환한다. 이 때 재귀함수에서는 반환된 거리 중 최솟값을 반환하게 구현한다.
BFS의 경우에는,
이전 게시물에서도 언급했듯이 층별로 자식노드가 null인 노드를 찾아서 바로 반환하기 때문에 DFS보다 더 효율적으로 문제를 해결할 수 있다.
이제 Tree말단 노드까지의 가장 짧은 경로를 DFS코드로 구현할 것이다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | class Node{ int data; Node lt, rt; public Node(int root){ data = root; lt = rt = null; } } public class Practice { public static Node root; public static int DFS(int L, Node root){ if(root.lt==null && root.rt==null) return L; else return Math.min(DFS(L+1, root.lt), DFS(L+1, root.rt)); } public static void main(String[] args){ root = new Node(1); root.lt = new Node(2); root.rt = new Node(3); root.lt.lt = new Node(4); root.lt.rt = new Node(5); System.out.println(DFS(0, root)); } } | cs |
재귀 함수의 종료 조건은 말단 노드인 경우이다.(왼/오른쪽 자식 노드가 모두 없는 경우에 종료된다)
스택 프레임을 그려서 DFS 작동방식을 더 깊게 알아볼 것이다.


'알고리즘' 카테고리의 다른 글
| 그래프와 인접행렬 (0) | 2022.12.11 |
|---|---|
| Tree 말단 노드까지의 가장 짧은 경로(BFS) (0) | 2022.12.11 |
| 이진트리 순회(너비우선탐색 : 레벨탐색) (2) | 2022.12.10 |
| 부분집합 구하기(DFS) (0) | 2022.12.10 |
| 이진트리 순회(깊이우선 탐색) (2) | 2022.12.10 |

level 0 : 1
level 1 : 2, 3
level 2 : 4, 5, 6, 7
왼쪽의 이진트리는 층별로 노드들이 이루어져 있다.
너비우선 탐색, BFS는 층별로 탐색을 한다. 수평적으로 탐색을 하기 때문에 순회 순서를 나타내면, 1-2-3-4-5-6-7 순서로 순회한다. BFS는 큐를 사용하여 탐색한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | class Node{ int data; Node lt, rt; public Node(int root){ data = root; lt = rt = null; } } public class Practice { public static Node root; public static Queue<Node> q; public static void BFS(){ while(!q.isEmpty()){ int len = q.size(); for(int i=0; i<len; i++){ Node cur = q.poll(); System.out.print(cur.data + " "); if(cur.lt!=null) q.offer(cur.lt); if(cur.rt!=null) q.offer(cur.rt); } } } public static void main(String[] args){ q = new LinkedList<>(); root = new Node(1); root.lt = new Node(2); root.rt = new Node(3); root.lt.lt = new Node(4); root.lt.rt = new Node(5); root.rt.lt = new Node(6); root.rt.rt = new Node(7); q.offer(root); BFS(); } } | cs |
위의 코드에서 변수 len은 층별로 담겨있는 노드의 개수를 뜻한다.

큐를 활용하여 설명하자면, 이진 트리의 최상위에 있는 노드를 먼저 큐에 넣고 시작하게 된다.
최상위 노드를 큐에서 빼낸 뒤 자식 노드가 있는지 검사를 한다. 있다면, 자식 노드들을 넣어준다.
위의 과정을 큐가 빌 때까지 반복하면 된다.
'알고리즘' 카테고리의 다른 글
| 그래프와 인접행렬 (0) | 2022.12.11 |
|---|---|
| Tree 말단 노드까지의 가장 짧은 경로(BFS) (0) | 2022.12.11 |
| Tree 말단 노드까지의 가장 짧은 경로(DFS) (0) | 2022.12.11 |
| 부분집합 구하기(DFS) (0) | 2022.12.10 |
| 이진트리 순회(깊이우선 탐색) (2) | 2022.12.10 |
자연수 N이 주어지면 1부터 N까지의 원소를 갖는 집합의 부분집합을 모두 출력하는 프로그램을 작성하시오.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | public class Practice { static int number; static boolean[] check; public void DFS(int n){ if (n == number + 1) { for (int i = 0; i < check.length; i++) { if (check[i]) System.out.print(i + " "); } System.out.println(); } else { check[n] = true; DFS(n + 1); check[n] = false; DFS(n + 1); } } public static void main(String[] args){ Practice pr = new Practice(); pr.number = 3; check = new boolean[number+1]; pr.DFS(1); } } | cs |

위의 코드는 아래와 같은 상태트리 구현으로 작성하였다.
N을 입력받으면 1부터 시작하여 부분집합에 넣는 경우(O)와 넣지 않는 경우(X)를 DFS로 구현하였다.
숫자 i를 넣는 경우에는 check[i]를 true로 바꾼 상태에서 DFS(i+1)를 호출하였고, 넣지 앟는 경우에는 check[i]를 false로 변경하여 DFS(i+1)을 호출하였다.
만약 DFS(N+1)이 호출된다면 check배열이 true인 값들로만 출력되게 하여서 부분집합의 경우를 모두 나타냈다.
'알고리즘' 카테고리의 다른 글
| 그래프와 인접행렬 (0) | 2022.12.11 |
|---|---|
| Tree 말단 노드까지의 가장 짧은 경로(BFS) (0) | 2022.12.11 |
| Tree 말단 노드까지의 가장 짧은 경로(DFS) (0) | 2022.12.11 |
| 이진트리 순회(너비우선탐색 : 레벨탐색) (2) | 2022.12.10 |
| 이진트리 순회(깊이우선 탐색) (2) | 2022.12.10 |
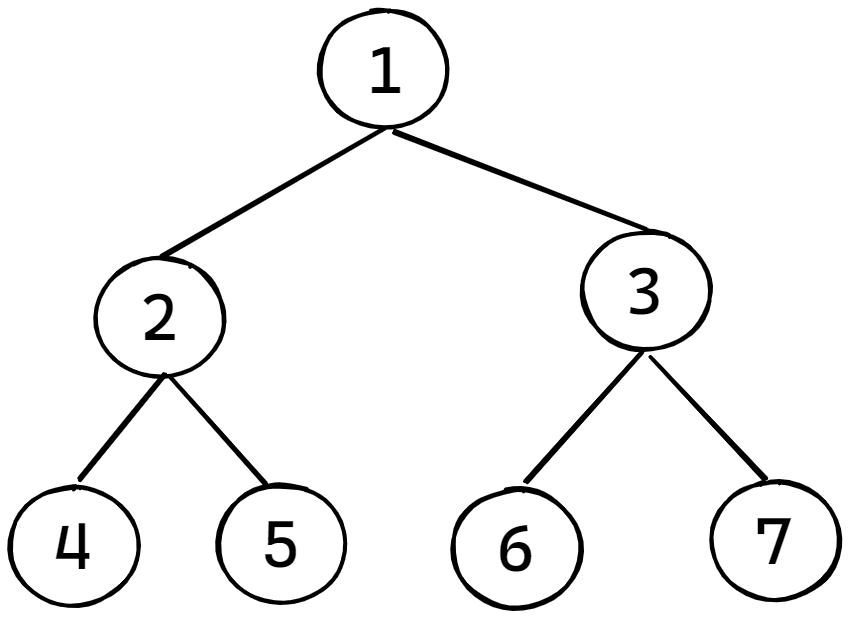
깊이우선 탐색(DFS)를 활용하여 이진트리를 순회할 수 있다.
순회 방법에는 (1)전위순회, (2)중위순회, (3)후위순회 이렇게 3가지의 방법이 있다.
트리는 기본 단위로 부모노드와 왼/오 자식노드를 가지고 있다.
전위 순회는 부모-왼-오 순서를 가지며, 중위 순회는 왼-부모-오 순서를 가진다. 후위 순회는 왼-오-부모 순서로 순회를 한다. 그림을 토대로 각각 순회 방법대로 적용한다면 아래와 같다.
전위 순회를 한다면, 1-2-4-5-3-6-7 순서로 순회를 한다.
중위 순회를 한다면, 4-2-5-1-6-3-7 순서로 순회를 한다.
후위 순회를 한다면, 4-5-2-6-7-3-1 순서로 순회를 한다.
이를 직접 코드로 구현을 하는 것이 포스팅의 목적이다.
Node클래스를 만들어서 int타입의 data와 왼/오 Node를 구성한다.
DFS메서드를 만들어서 재귀 호출을 하게 구현하였다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | class Node{ int data; Node lt, rt; Node(int val){ data = val; lt=rt=null; } } public class Practice { Node root; public void DFS(Node root){ if(root==null) return; else{ //System.out.print(root.data + " "); - 전위 순회 DFS(root.lt); //System.out.print(root.data + " "); - 중위 순회 DFS(root.rt); //System.out.print(root.data + " "); - 후위 순회 } } public static void main(String[] args){ Practice pr = new Practice(); pr.root = new Node(1); pr.root.lt = new Node(2); pr.root.rt = new Node(3); pr.root.lt.lt = new Node(4); pr.root.lt.rt = new Node(5); pr.root.rt.lt = new Node(6); pr.root.rt.rt = new Node(7); pr.DFS(pr.root); } } | cs |
위의 코드에서 보면 알 수 있듯이, 출력 메서드가 어디에 위치하느냐에 따라 순회의 결과가 변경되어 나타난다.
이는 재귀함수의 동작을 스택 프레임과 연관지어 생각하면 원리를 이해할 수 있다.
스택프레임(Stack Frame)이란?
함수가 호출될 때마다, LIFO 스택에 적재되는 방식으로 생성된다. 스택 프레임에는 함수와 관계되는 지역변수(local variables), 매개변수(parameters), 복기 주소(return address)로 구성되어 있다.
복기 주소는 스택의 상위 스택 프레임이 실행되고 나서 돌아갈 주소를 담고 있는 것이다.
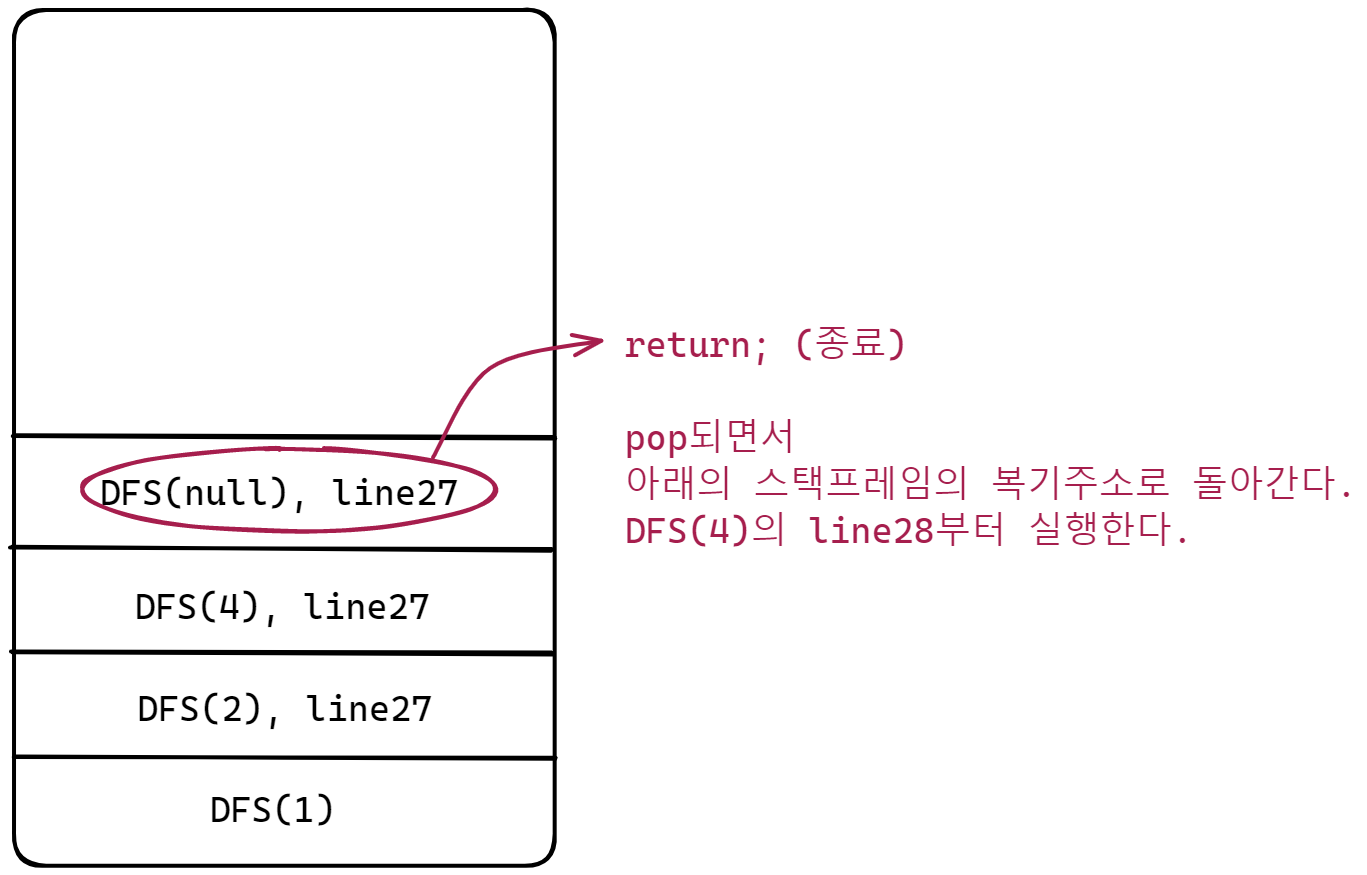
DFS(4)가 호출되어 스택프레임에 쌓이고 다시 DFS메서드를 실행한다.
Node의 data가 4일 때에는 왼쪽, 오른쪽 자식 노드가 모두 null값을 가지고 있다.
DFS(null)이 호출되고 코드를 작동하는데 if 조건문에 걸리게 되어 return하여 pop된다.
다시 DFS(4)의 오른쪽 자식 노드를 호출하는데 이것도 null이므로 위의 과정을 반복한다.
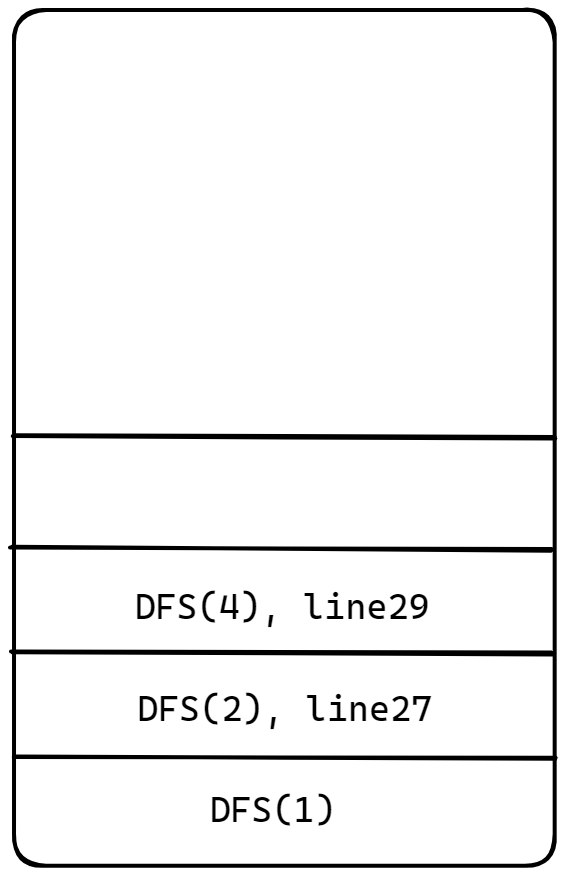
DFS(4)의 자식 노드를 호출하는 DFS메소드가 모두 pop된 다음, DFS(4)의 복기주소로 돌아가 수행하려하는데 마지막 출력메서드만 남았다. 그러므로 4를 출력해준 다음 DFS(4)는 종료되어 pop이 된다. 그리고 다시 DFS(2)메소드의 line28부터 수행한다.
'알고리즘' 카테고리의 다른 글
| 그래프와 인접행렬 (0) | 2022.12.11 |
|---|---|
| Tree 말단 노드까지의 가장 짧은 경로(BFS) (0) | 2022.12.11 |
| Tree 말단 노드까지의 가장 짧은 경로(DFS) (0) | 2022.12.11 |
| 이진트리 순회(너비우선탐색 : 레벨탐색) (2) | 2022.12.10 |
| 부분집합 구하기(DFS) (0) | 2022.12.10 |
1. 인프런 코테 강의 학습하며, 블로그에 풀이 적기
2. 자소서 틀 구체화시키기
'daily > 2022.12' 카테고리의 다른 글
| 2022.12.06 (0) | 2022.12.06 |
|---|---|
| 2022.12.04 (0) | 2022.12.04 |
- 인프런 DP/DFS/BFS 풀이, 강의시청, 오답노트
- dnd 자소서 쓰기
- Comparator, Comparable 노션 정리
'daily > 2022.12' 카테고리의 다른 글
| 12월 목표 (0) | 2022.12.06 |
|---|---|
| 2022.12.04 (0) | 2022.12.04 |
1. 인프런 dp문제 풀기, 비디오 시청
2. 네트워크 공부기록 작성
3. 알고리즘 문풀 다시 복습 및 정리
4. dnd 자소서 작성
'daily > 2022.12' 카테고리의 다른 글
| 12월 목표 (0) | 2022.12.06 |
|---|---|
| 2022.12.06 (0) | 2022.12.06 |
목표
- 오류 추정을 설명할 수 있다
- 탐색적 테스팅을 설명할 수 있다
- 체크리스트 기반 테스팅을 설명할 수 있다
1. 오류 추정(= 결함을 추정한다), 오류/결함 및 장애 발생을 예측하는 기술
접근법 - 테스터의 지식과 경험 또는 결함 및 장애 데이터를 기반으로, 발생 가능한 오류/결함/장애 목록을 작성하고, 장애와 그것의 원인이 되는 결함을 노출하는 테스트를 설계한다.
2. 탐색적 테스팅(경험기반 테스트에서 가장 중요!!)
- 비공식(사전에 정의되지 않은, 테케를 미리 만들어놓지 않은) 테스트를 테스트 실행 중에 동적으로 설계/실행/기록/평가한다
+ 명세기반기법에서는 테케를 미리 만들어 놓는다 - 세션 기반 테스팅을 사용하여 활동을 구성한다. 탐색적 테스팅을 정해진 시한(time-box)동안 수행한다. 제한시간동안 몰입하여 테스트를 수행한다
- 첫번째 세션의 테스트 결과는 컴포넌트나 시스템에 대해 더 많이 학습하고, 더 많은 테스트가 필요한 영역에 대한 테스트를 작성하는 데 활용한다
- 테스트 차터 : 테스트 목적이 포함된 문서이다. 이를 기반으로 테스팅 방향을 설정한다. 명세 기반(블랙박스) 기법의 테스트 컨디션과 유사하다.
- 테스트 세션 시트 : 수행 단계와 발견 사항을 기록한 문서이다. 명세 기반(블랙박스) 기법의 테스트 로그와 유사하다.
- 명세가 충분하지 않거나 적은 경우 또는 테스팅에 상당한 시간적 압박이 있을 때 매우 유용하며, 다른 공식적인 테스팅 기법을 보완하는 데도 유용하다
3. 체크리스트 기반 테스팅(엑셀로 작성될 확률이 높다)
- 체크리스트에 기록된 테스트 컨디션을 커버하기 위해 테스터가 테스트를 설계/구현/실행한다
- 체크리스트 : 경험, 사용자에게 무엇이 중요한지에 대한 지식 또는 소프트웨어가 실패하는 이유와 방법에 대한 이해를 기반으로 작성한다. 기능 및 비기능 테스팅을 포함한 다양한 테스트 유형을 지원하기 위해 작성한다.
- 구체적인 테케가 없는 경우, 대략적인 지침과 일관성을 제공한다
- 상위 수준의 체크리스트는 커버리지는 높일 수 있겠지만, 재현 가능성이 줄어들 수 있다
테스트 기법의 선택
- 일부 기법은 특정 상황과 테스트 레벨이 더 적합한 반면, 모든 테스트 레벨에 적합한 기법도 있다
기법 선택 시 고려 사항
- 컴포넌트나 시스템의 복잡도
- 규제 기준, 고객 또는 계약 요구사항
- 리스크 수준과 유형 ( 리스크 수준이 높을 수록 강한 기법을 사용한다)
- 사용 가능한 문서
- 테스터의 지식과 역량
- 사용 가능 도구
- 시간, 예산
- 소프트웨어 개발 수명주기 모델
- 예상되는 결함 유형




